Some Old Friends and the Games We Can Play With Them

It’s the start of a new school year. We’re seeing our friends whom we haven’t seen all summer long. We’re making new friends. We’re excited to again get to play all of our favorite games with our friends. But this is Nueva, and so our friends are not people, but rather abstract objects. In particular, our friends are functions. And the games we want play with them aren’t chess or dodgeball or backgammon—the games we want to play are those called linear transformations.¹

Let’s back up a bit. Here’s what we’re going to be thinking about for the first few weeks of our class. How can we take equations and turn them into pictures?

\[\text{equations} \longrightarrow \text{pictures}\]

How can we take pictures and turn them into equations?

\[\text{equations} \longleftarrow \text{pictures}\]

How can we do this in both directions, back and forth, back and forth, over and over again, without a calculator, using only our minds, so that we develop a deep intuition for what equations look like? In other words, we’re trying to figure out this:

\[\text{equations} \Longleftrightarrow \text{pictures}\]

We’re going to try to become algebraic synæsthetes². Synæsthesia, as you might know, is the neurological condition describing when your senses overlap—when you can see sounds, or smell colors, or associate words with physical sensations. Your senses get all mixed up. That’s what we want. We want no difference between seeing a picture and seeing an equation.

To start acquiring our algebraic synæsthesia, let’s learn (or remind ourselves of) some basic functions and their shapes, and then figure out hw we can change them in simple ways. How can we move them up and down and left and right? How can we stretch them out? How can we squeeze and compress them? How can we flip them around? How does changing their equations change their pictures? How does changing their pictures change their equations?

It’s the start of a new year, so let’s make some new friends—or reintroduce ourselves to some old friends. Let’s list a dramatis personae of the characters who will populate our story:

\[f(x) = x\]

• A line with slope \(1\) and \(y\)-intercept \(0\), passing through the origin at \((0,0)\)
• Extremely boring!!!
• The fancy mathematical word for this function is that it’s the identity function, or even fancier, that it’s idempotent

\[f(x) = x^2\]

• Passes through \((0,0)\)
• Cool parabolic shape!
• Passes through \((-1,+1)\), the origin, and \((1,1)\)
• (What’s the difference between \(x^2\), \(x^4\), \(x^6\), etc.? What happens to \(x^n\) as \(n\) gets bigger?)

\[f(x)=x^3\]

• Cool twisty shape
• Passes through \((-1,-1)\), the origin, and \((1,1)\)
• Flat for a moment at the origin!
• (What’s the difference between \(x^3\), \(x^5\), \(x^7\), etc.? What happens to \(x^n\) as \(n\) gets bigger?)

\[f(x)=\frac1x\]

• Also known as \(f(x) = x^{-1}\)
• Pretty symmetry!
• Vertical asymptote at \(x=0\) (but in different directions from each side)
• Horizontal asymptotes at \(y=0\)
• Passes through \((-1,-1)\) and \((+1,+1)\)
• (What’s the difference between \(1/x^3\), \(1/x^5\), \(1/x^7\), etc.? What happens to \(1/x^n\), where \(n\) is some odd positive integer, as \(n\) gets bigger?)

\[f(x)=\frac{1}{x^2}\]

• An infinitely-tall volcano! (Alternatively: a infinitely-tall redwood!)
• Also known as \(f(x) = x^{-2}\)
• Vertical asymptote at \(x=0\) and horizontal asymptotes at \(y=0\)
• Passes through \((-1,+1)\) and \((+1,+1)\)
• (What’s the difference between \(1/x^2\), \(1/x^4\), \(1/x^6\), etc.? What happens to \(1/x^n\), where \(n\) is some even positive integer as \(n\) gets bigger?)

\[f(x)=\sqrt{x}\]

• The square root function (or at least, the positive square root)
• Also known as \(f(x)=x^{1/2}\)
• Doesn’t exist when \(x<0\) (UNLESS YOU BELIEVE IN IMAGINARY NUMBERS!!!)
• Passes through \((1,1)\); touches the origin at \((0,0)\) (but stops there).

\[f(x)=\sqrt[3]{x}\]

• The cube root!
• Also known as \(x^{1/3}\)
• Exists for all values of \(x\), unlike the square root (why? why can we take the cube roots of negative numbers?)
• Passes through the origin at \((0,0)\), also passes through \((1,1)\), and even \((-1,-1)\)!

\[f(x)=e^x\]

• An exponential function, with base \(e \approx 2.71...\)
• Long horizontal asymptote to \(y=0\) on the left!
• On the right, keeps going up forever and ever, getting steeper and steeper!
• Passes through \((0,1)\) and \((1,e)\)
• (How does this differ from {} exponential functions with different bases, like \(f(x)=5^x\) or \(f(x)=3^x\) or \(f(x)=(1/2)^x\)???)

\[f(x)=\ln(x)\]

• The “natural logarithm,” i.e., a logarithm with base \(e\)
• Doesn’t exist when \(x<0\) (UNLESS YOU BELIEVE IN IMAGINARY NUMBERS!!!)
• Vertical asymptote at \(x=0\)
• Passes through \((1,0)\) and \((e,1)\)
• Keeps going up and to the right forever and ever… just less and less steeply and more and more flat-ly.
• We’ll talk a lot more about logarithms and exponentials later!
• (Are there other logarithms????)

\[f(x) = \sin(x)\]

• A trig function!
• Repeats every \(2\pi\) (= \(360^\circ\))
• \(x\)-intercepts at \(\pi \pm k\pi\), where \(k\) is any integer, i.e. \(\pm \pi, \pm 2\pi, \pm 3\pi\), etc.
• Maxima at \(\frac{\pi}{2} \pm 2k\pi\), i.e. at \(x=\pi/2, \pm 5\pi/2, \pm9\pi/2\), etc.
• Minima at \(\frac{3\pi}{2} \pm 2k\pi\)

\[f(x) = \cos(x)\]

• Another trig function!
• Just like sine, but shifted a bit (how much? in which direction?)
• Repeats every \(2\pi\) (= \(360^\circ\))
• \(x\)-intercepts at \(\pi/2 \pm k\pi\), where \(k\) is any integer, i.e. \(\pm \pi/2\), \(\pm 3\pi/2\), \(\pm 5\pi/2\).

\[f(x) = \tan(x)\]

• Another trig function, but really different from sine and cosine
• Repeats every \(\pi\) (= \(180^\circ\)) (unlike sine and cosine)
• Vertical asymptotes at \(\pi/2 \pm k\pi\)
• \(x\)-intercepts at \(\pm k\pi\), where \(k\) is any integer, i.e. \(\pm \pi\), \(\pm2\pi\), \(\pm 3\pi\), etc.

So. Those are our friends. What are the games we can play with them?

Vertical transformations

Vertical shifts

• If we have the function \(f(x)\), and some positive number \(h\), then the graph of \(f(x) + h\) is the graph of \(f(x)\) moved up by \(h\) units.

Likewise, the graph of \(f(x)-h\) is the graph of \(f(x)\) moved down by \(h\) units.

\end{itemize}

Vertical expansions and contractions

Vertical reflections

Horizontal transformations

Horizontal shifts

Horizontal expansions and contractions

Horizontal reflections

Order of operations

Note that it matters in what order we apply these transformations! If we have \(f(x)\), and we want to draw \(af(bx + c) + d\), then we need to:

1. Shift left or right by \(c\)
2. Horizontally expand or contract by a factor of \(b\)
3. Vertically expand or contract by a factor of \(a\)
4. Vertically shift up or down by \(d\)

Problems

Let’s go from equations to pictures! For each of the following problems:

1. Identify the parent function
2. Write the transformed function in terms of the parent function
3. List the transformations, in order.
4. Graph the parent function
5. Graph the transformed function. (A nice way to do this would be to graph both the parent and transformed function on the same axes, but using different colors.)

Don’t use a graphing calculator—do this all by hand! I mean, you can use Desmos to check or something, if you want, but we’re trying to learn how to do all this {} in our heads, {}. There’s no need to draw a particularly precise picture—we’re just trying to get a {} for how these things work.

And, as an example of what I mean in (2), if you’re given \(f(x) = 3\sin(x+2) - 7\), then you could set the parent function equal to \(g(x) = \sin(x)\), and then write \(f(x)\) as \(f(x) = 3g(x + 2) - 7\). This can make it a little easier to see the transformations—all the details of the function are stripped/abstracted and we’re left with just the transformations.

1. \(f(x) = e^x + 3\)
2. \(f(x) = \sin(x - \pi)\)
3. \(f(x) = 5x^2\)
4. \(f(x) = 3x^8\)
5. \(f(x) = -x^3\)
6. \(f(x) = (4x)^7\)
7. \(f(x) = \sqrt{-x}\)
8. \(f(x) = \sqrt{x} + 4\)
9. \(f(x) = 3x + 2\)
10. \(f(x) = \frac{1}{2}\ln(x)\)
11. \(f(x) = \frac{1}{3x}\)
12. \(f(x) = \cos(5x)\)
13. \(f(x) = 12\) 
14. \(f(x) = - x^2\)
15. \(f(x) = x - 5\)
16. \(f(x) = \sqrt{x + 4}\)
17. \(f(x) = \left(\frac{x}{4}\right)^3\)
18. \(f(x) = \frac{-1}{x}\)
19. \(f(x) = \sqrt[3]{-x}\)
20. \(f(x) = 5\)
21. \(f(x) = 3x\)
22. \(f(x) = 2x + 1\)
23. \(f(x) = -(x - 5) + 3\)
24. \(f(x) = 2x+1\)
25. $f(x) = x - 5 $
26. $f(x) = - x $
27. \(f(x) = -2x + 5\)
28. \(p(y) = 4(y + 1) - 6\)
29. \(f(x) = -2x^2\)
30. \(f(x) = 9x^2\)
31. \(f(x) = (3x)^2\)
32. \(f(x) = 3x^2 - 4\)
33. \(f(x) = (x + 4)^2\)
34. \(f(x) = (-x)^2\)
35. \(f(x) = (4x - 2)^2\)
36. \(f(x) = -(-3x - 7)^2\)
37. \(f(x) = \frac{1}{3}(5x + 9)^2 - 14\)
38. \(g(x) = (x-1)^2\)
39. \(s(x) = -x^4 + 2\)
40. \(f(x) = -(x^4 - 2)\)
41. \(f(x) = -(x-3)^4\)
42. \(f(x) = x^6 - 2\)
43. \(f(x) = (x + 2)^3\)
44. \(f(x) = x^3-1\)
45. \(f(x) = (-x)^3\)
46. \(f(x) = -x^3\)
47. \(f(x) = -3(x + 1)^3\)
48. \(f(x) = \frac{1}{5}(x - 2)^3 - 4\)
49. \(f(x) = 9(-x + 6)^3 - 1\)
50. \(f(x) = (x+2)^3+1\)
51. \(f(x) = x^7 + 5\)
52. \(f(x) = \sqrt{x - 3}\)
53. \(f(x) = -\sqrt{x}\)
54. \(f(x) = \sqrt{-x}\)
55. \(f(x) = -4\sqrt{2x + 1}\)
56. \(f(x) = \sqrt{-x + 7}\)
57. \(f(x) = \sqrt{-x + 1} - 2\)
58. $f(x) = 4 - 2 $
59. \(f(x) = \sqrt[3]{-x} - 5\)
60. \(f(x) = 6\sqrt[3]{x + 5}\)
61. \(f(x) = \sqrt[3]{x + 3} + 2\)
62. \(f(x) = \sin(x + \pi/2)\)
63. \(f(x) = 5\sin(x)\)
64. \(f(x) = \sin(5x)\)
65. \(f(x) = 5\sin(5x)\)
66. \(f(x) = \cos(x + 3\pi)\)
67. \(f(x) = 2\cos(x) + 2\)
68. \(f(x) = \frac{1}{2}\sin(x)\)
69. \(f(x) = -\sin(x) + 1\)
70. \(f(x) = \cos(-x) - 1\)
71. \(f(x) = -3\cos(4x + 2\pi) + 5\)
72. \(b(\theta) = 5\sin{(3\theta + \pi)}\)
73. \(f(x) = -2\sin{(-2x - \frac{3}{4}\pi)}\)
74. \(f(x) = 2\sin(x)\)
75. \(f(x) = \sin(2x)\)
76. \(f(x) = \sin(x + \pi/2)\)
77. \(r(x) = -12\tan(x)\)
78. \(f(x) = 2\cos(x + 2\pi)\)
79. \(f(x) = \cos(x + \pi)\)
80. \(f(x) = -\cos(x)\)
81. $f(x) = 4+ (1/x) $
82. \(\displaystyle f(x) = \frac{2}{x}\)
83. \(\displaystyle f(x) = \frac{1}{x + 3}\)
84. \(\displaystyle d(z) = \frac{-1}{z + 2}\)
85. \(\displaystyle f(x) = \frac{-1}{3x} + 5\)
86. \(\displaystyle f(x) = 3\cdot \frac{1}{5x}\)
87. $f(x) = $
88. \(t(x) = e^{x - 2} - 4\)
89. \(r(x) = 5e^{2x} + 1\)
90. \(w(y) = -e^{y + 2}\)
91. $f(x) = 12e^{-3x} $
92. $j(r) = e^{0.2r} $
93. \(h(x) = \ln{(x)} + 1\)
94. \(t(x) = \ln{x - 2.5} - 8\)
95. \(r(x) = \frac{1}{2}\ln{(3x)} + 1\)
96. \(w(y) = -\ln{(y + 6)}\)
97. $f(x) = 12 $
98. $j(r) = $

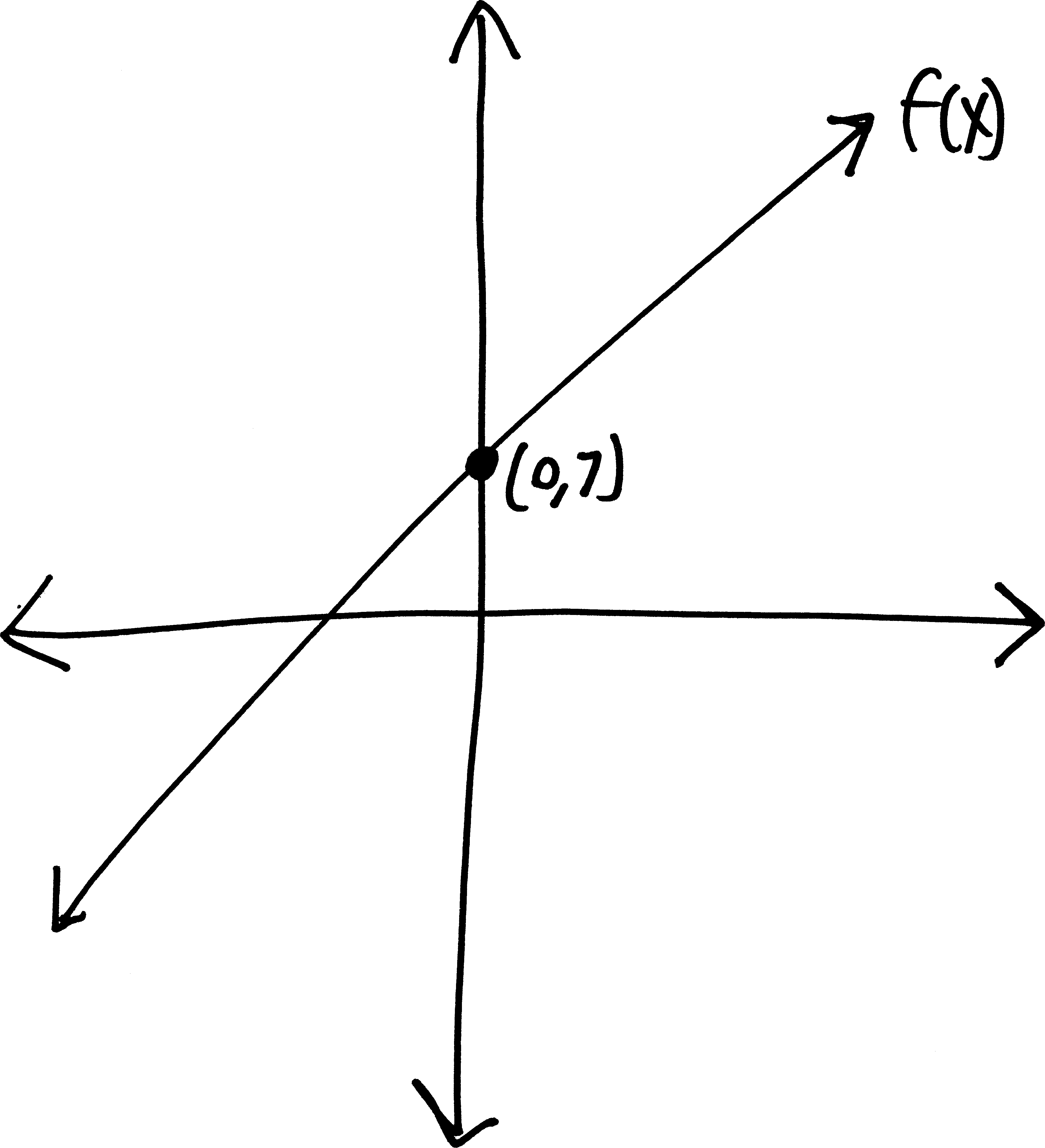
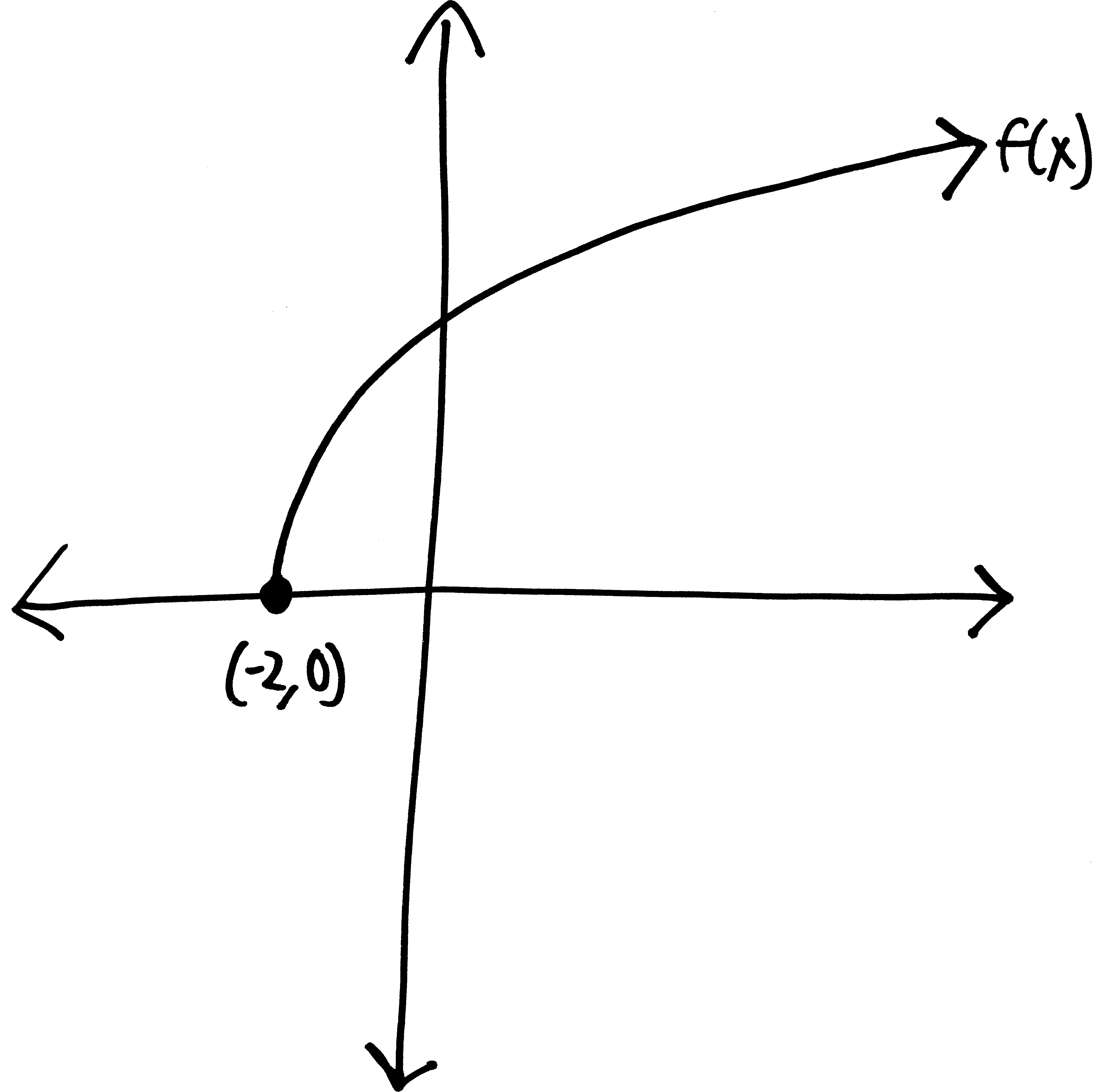
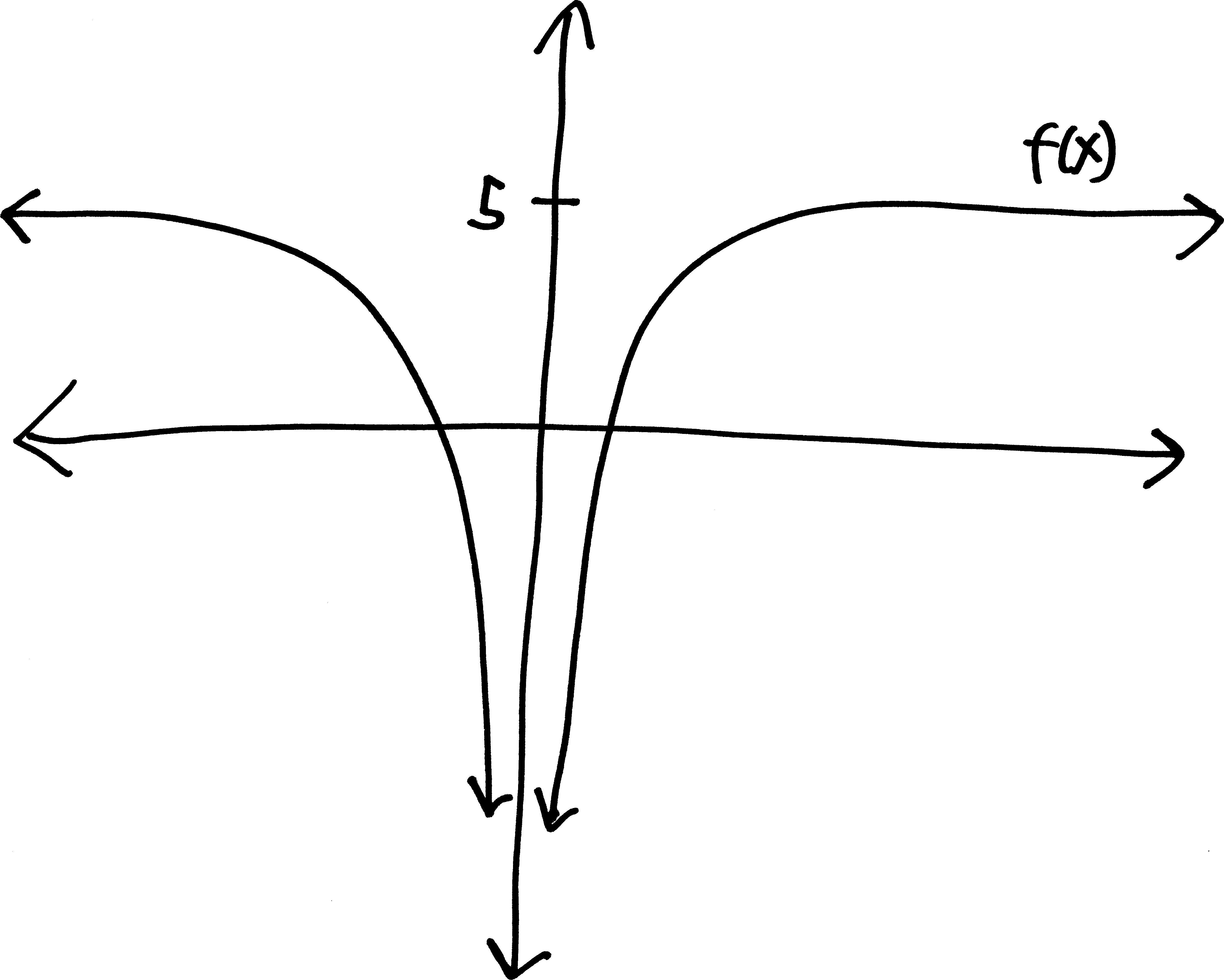
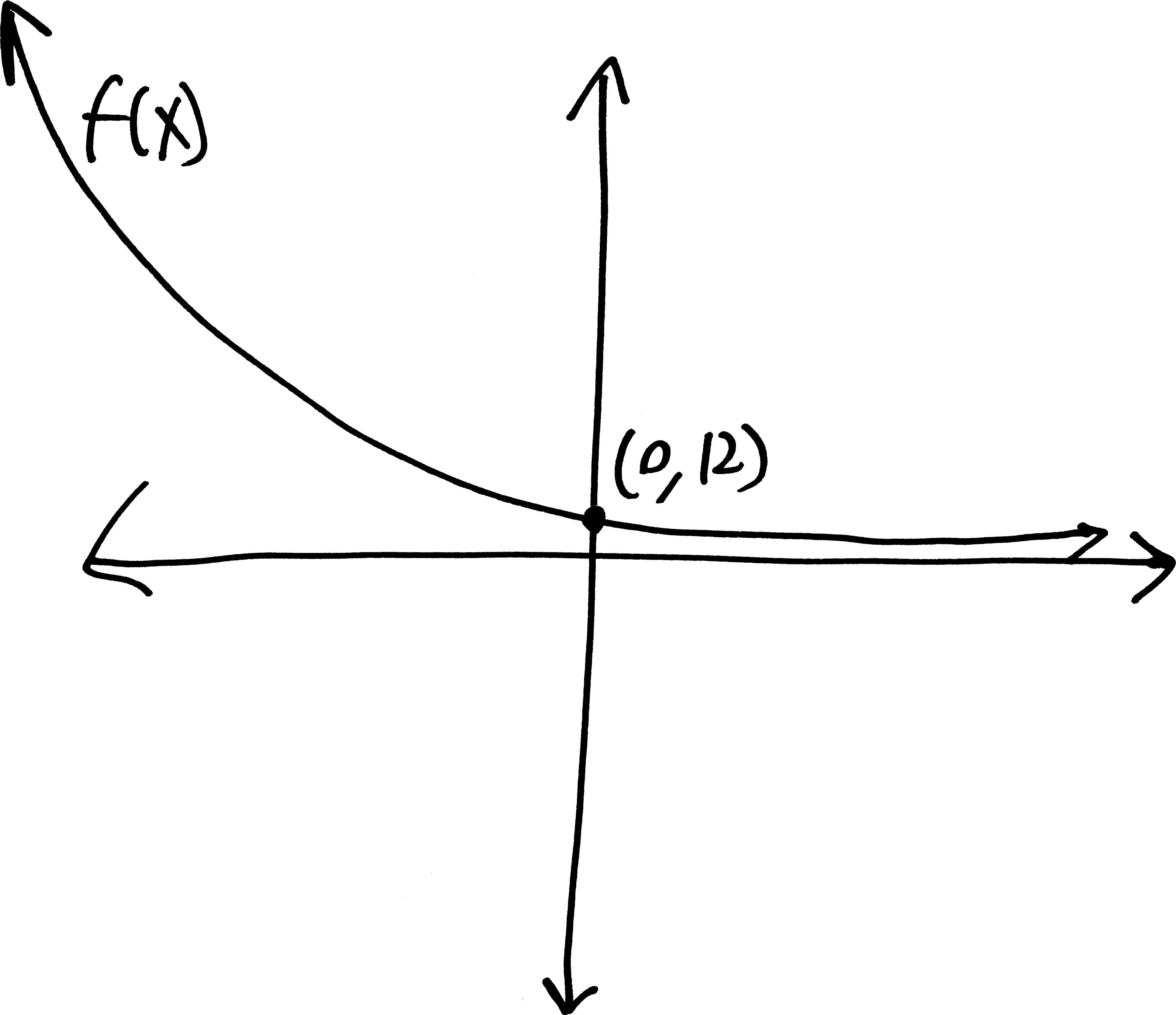
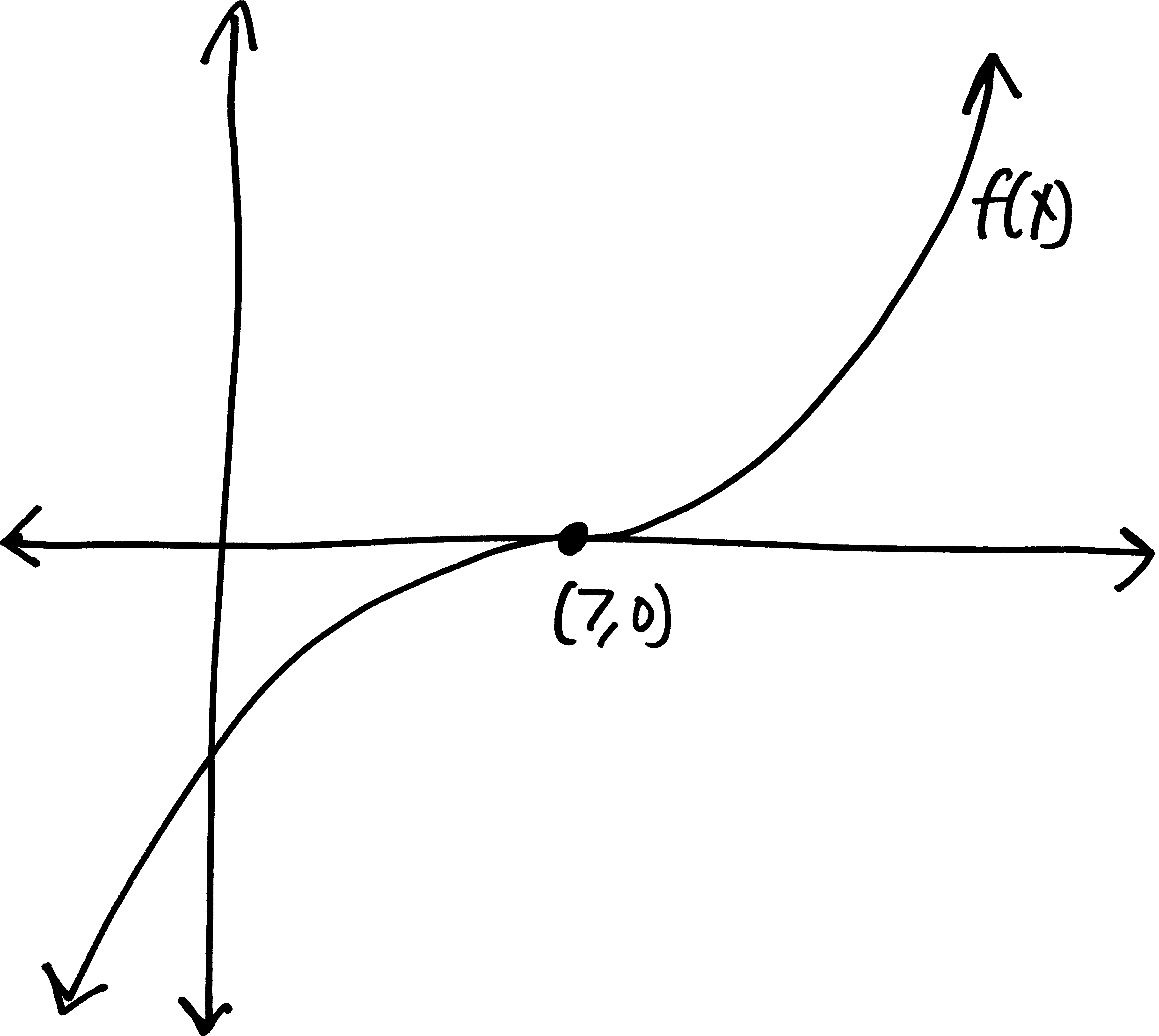
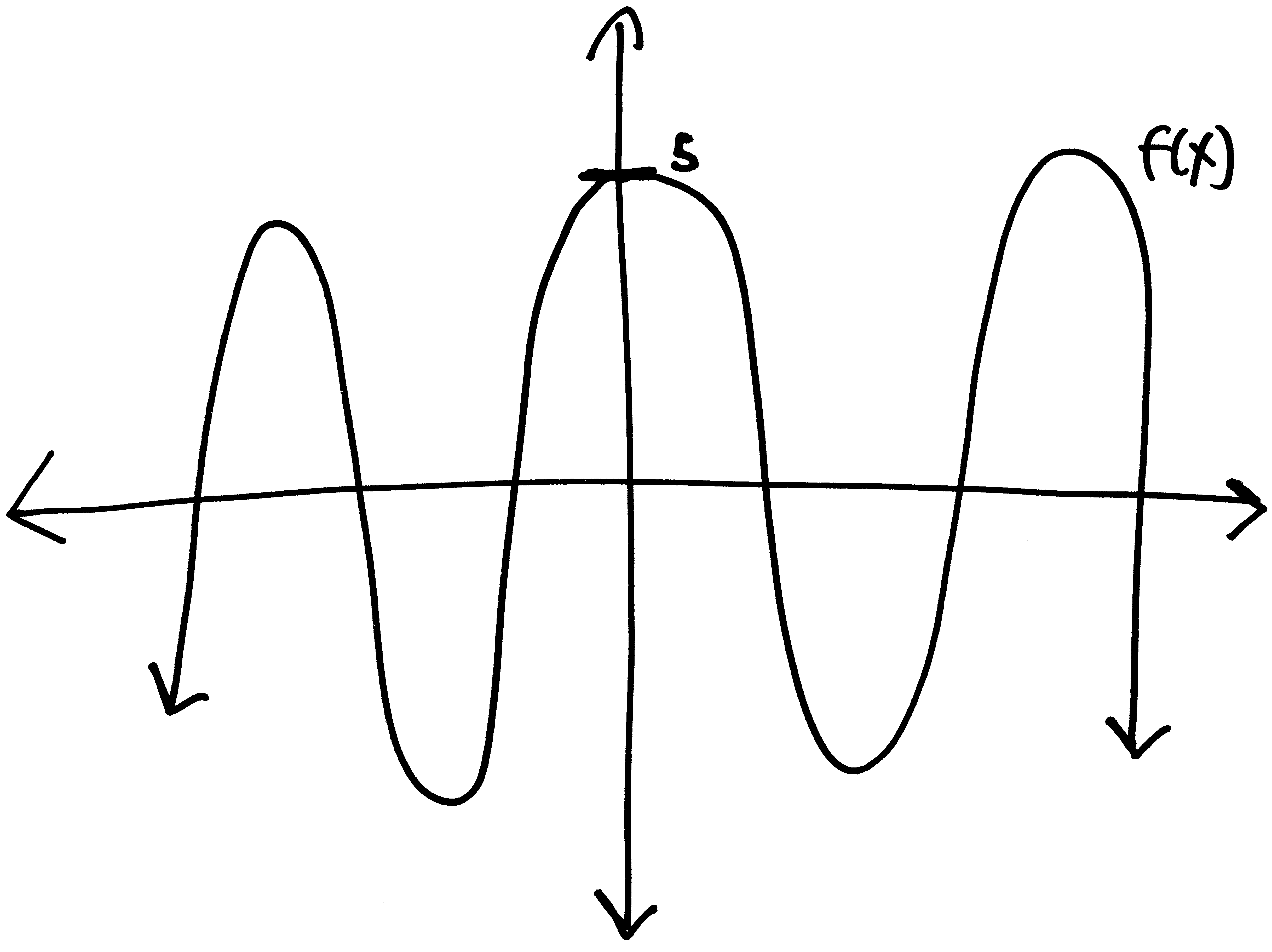
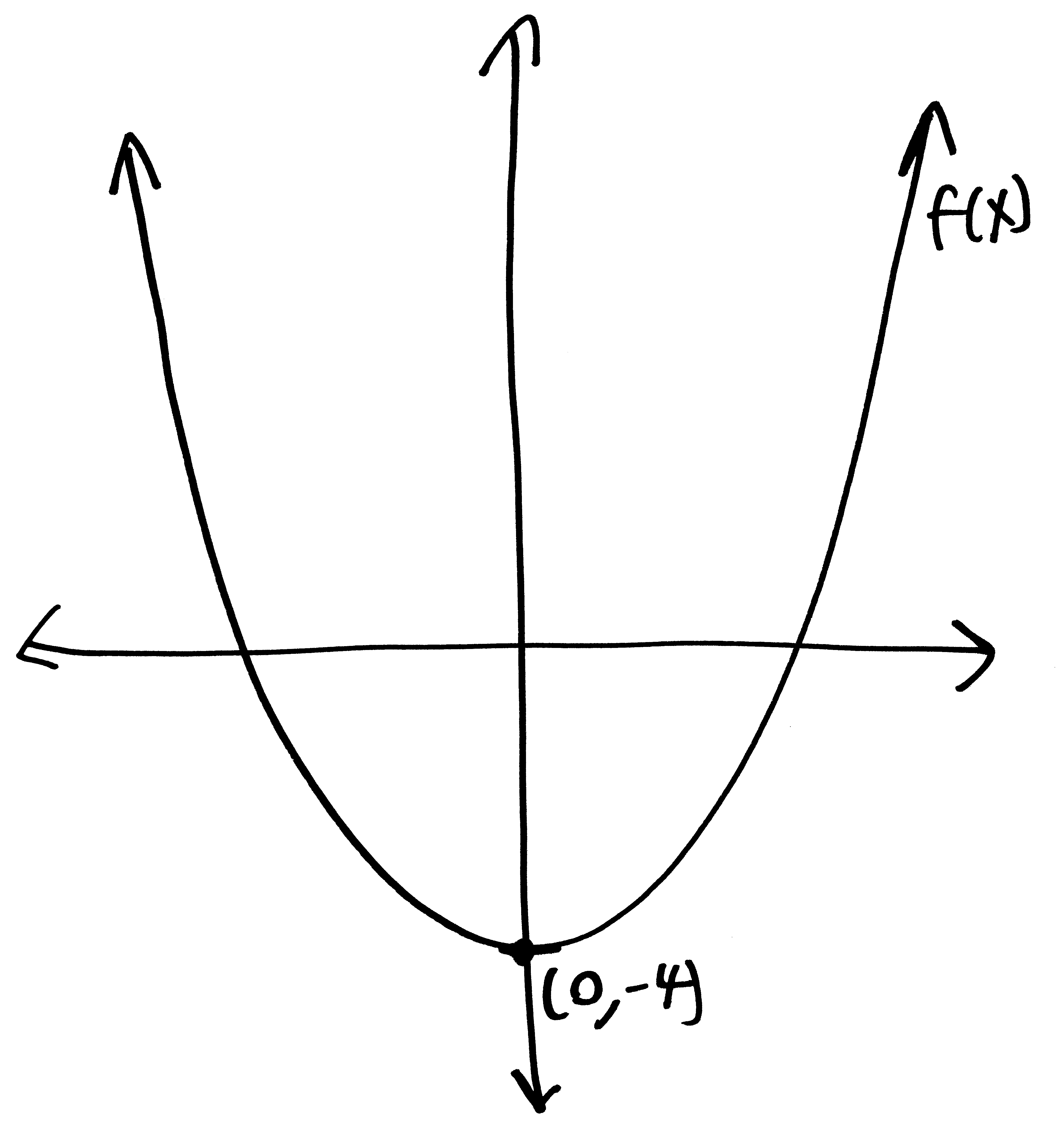
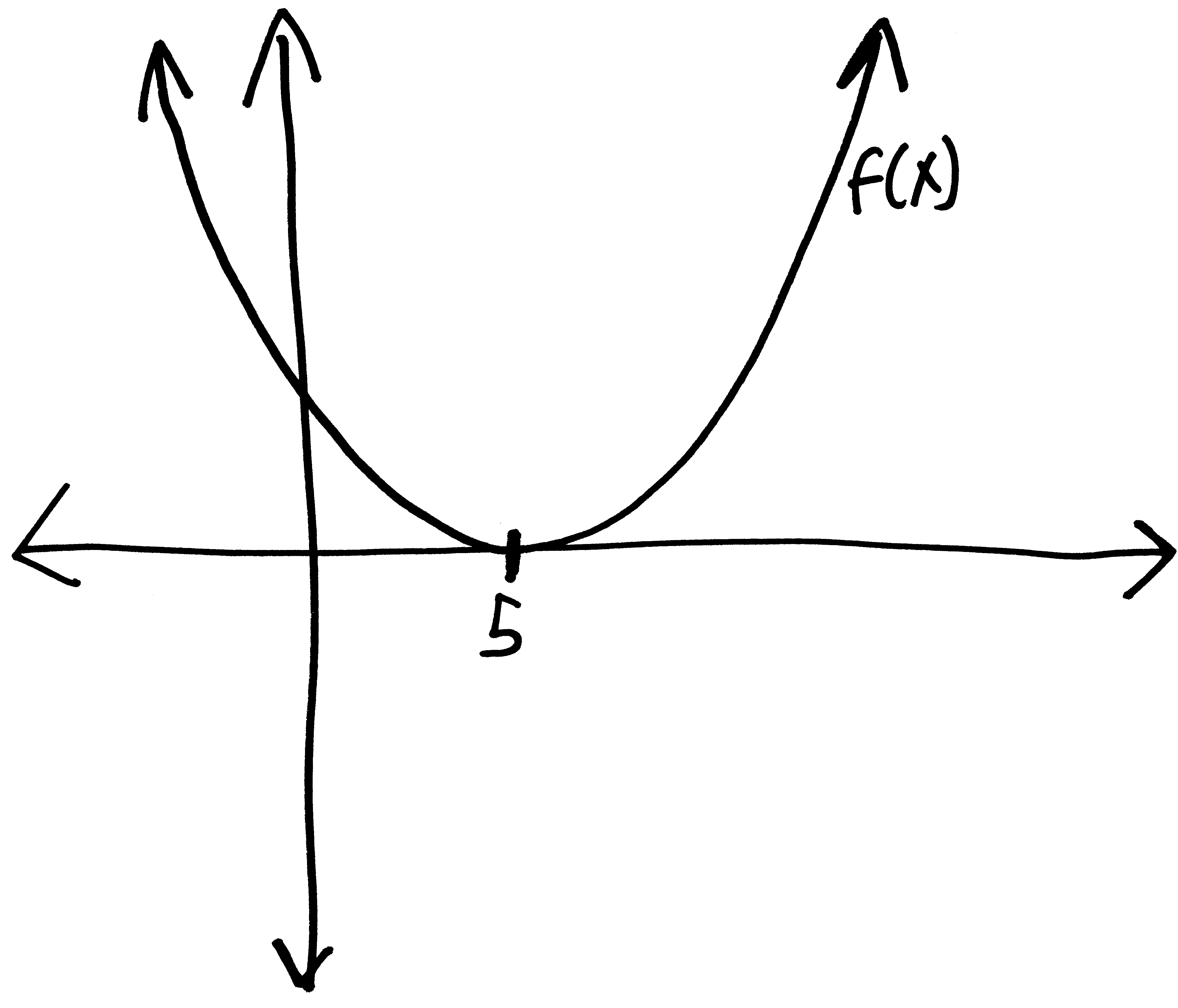
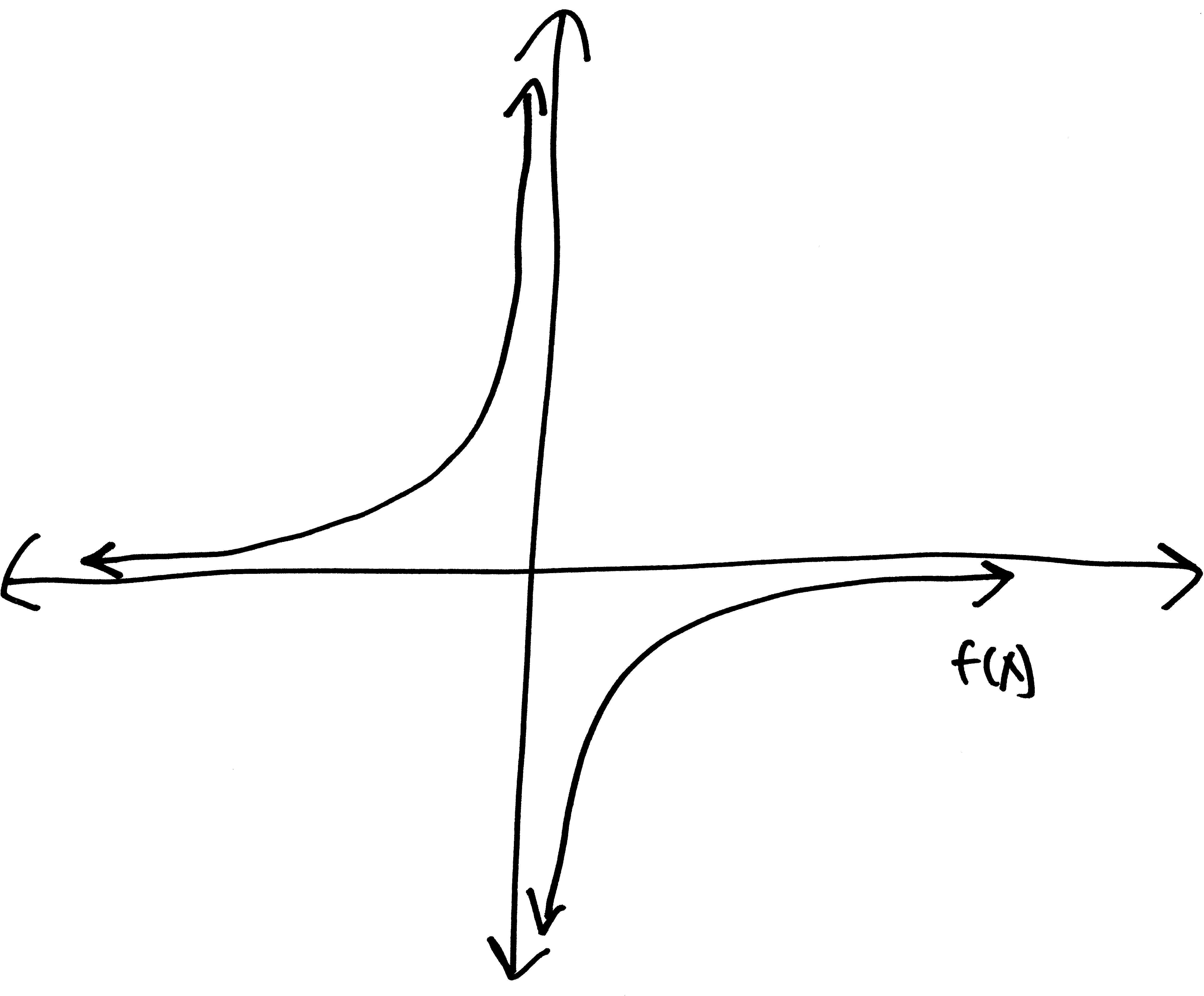
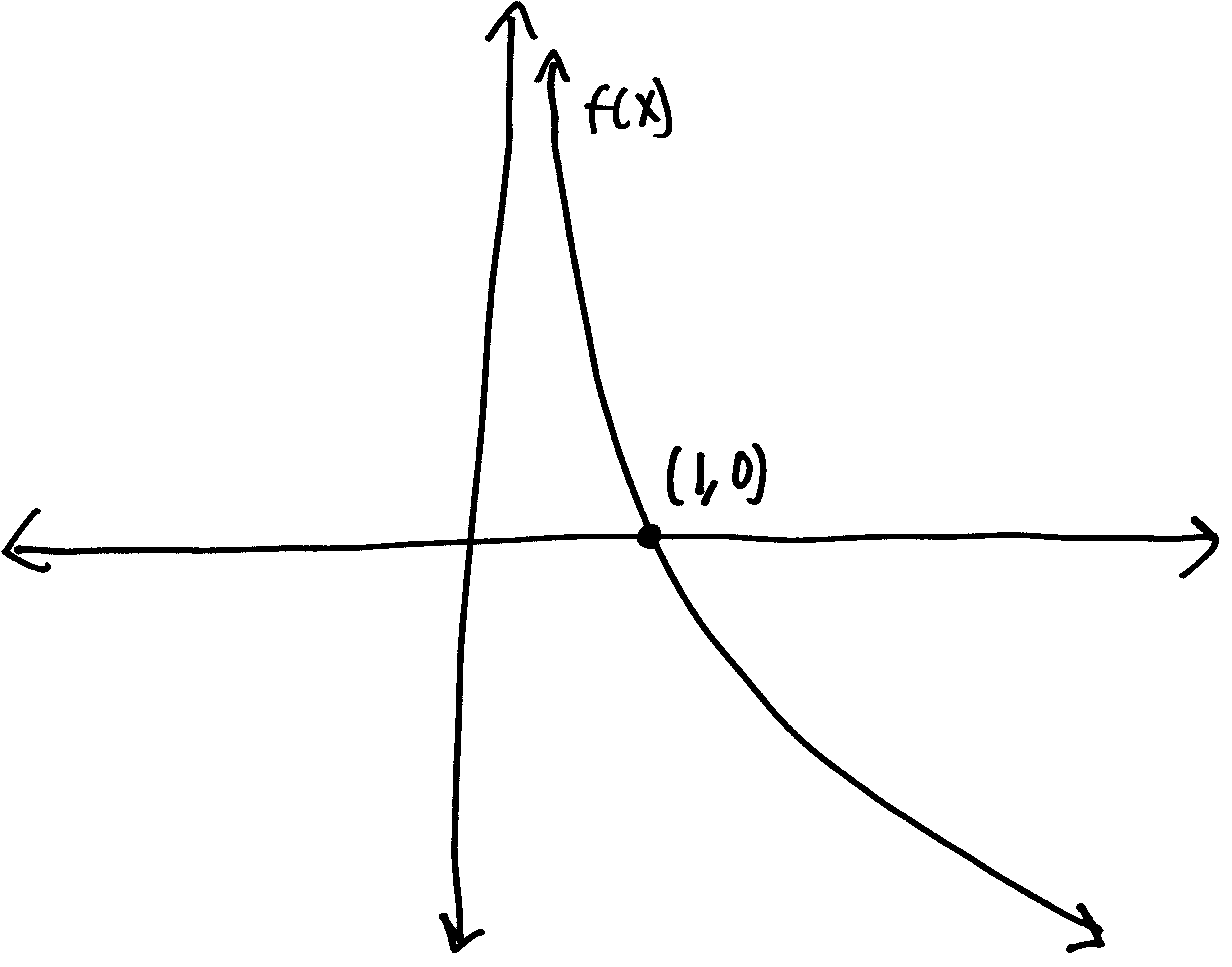
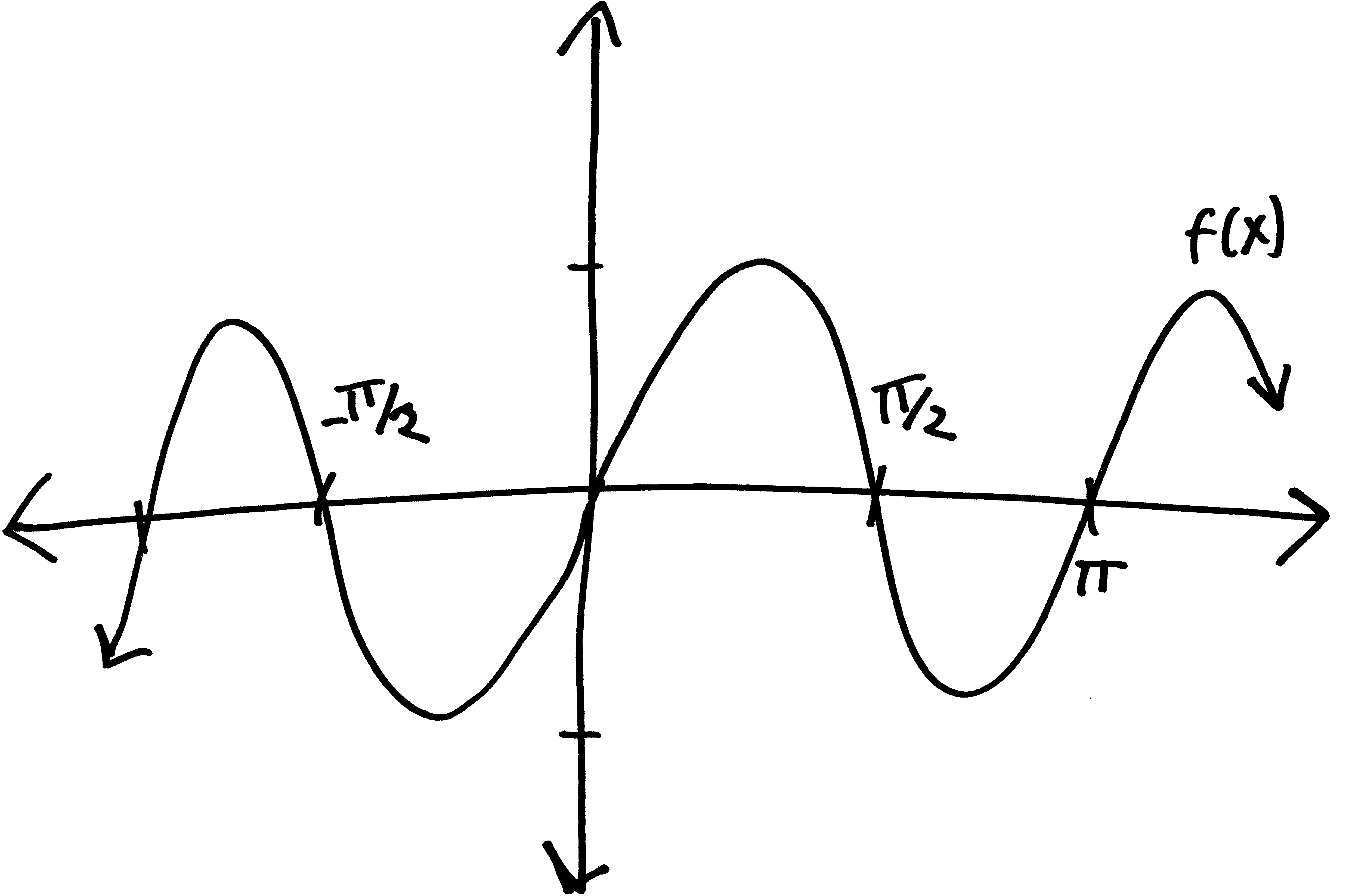
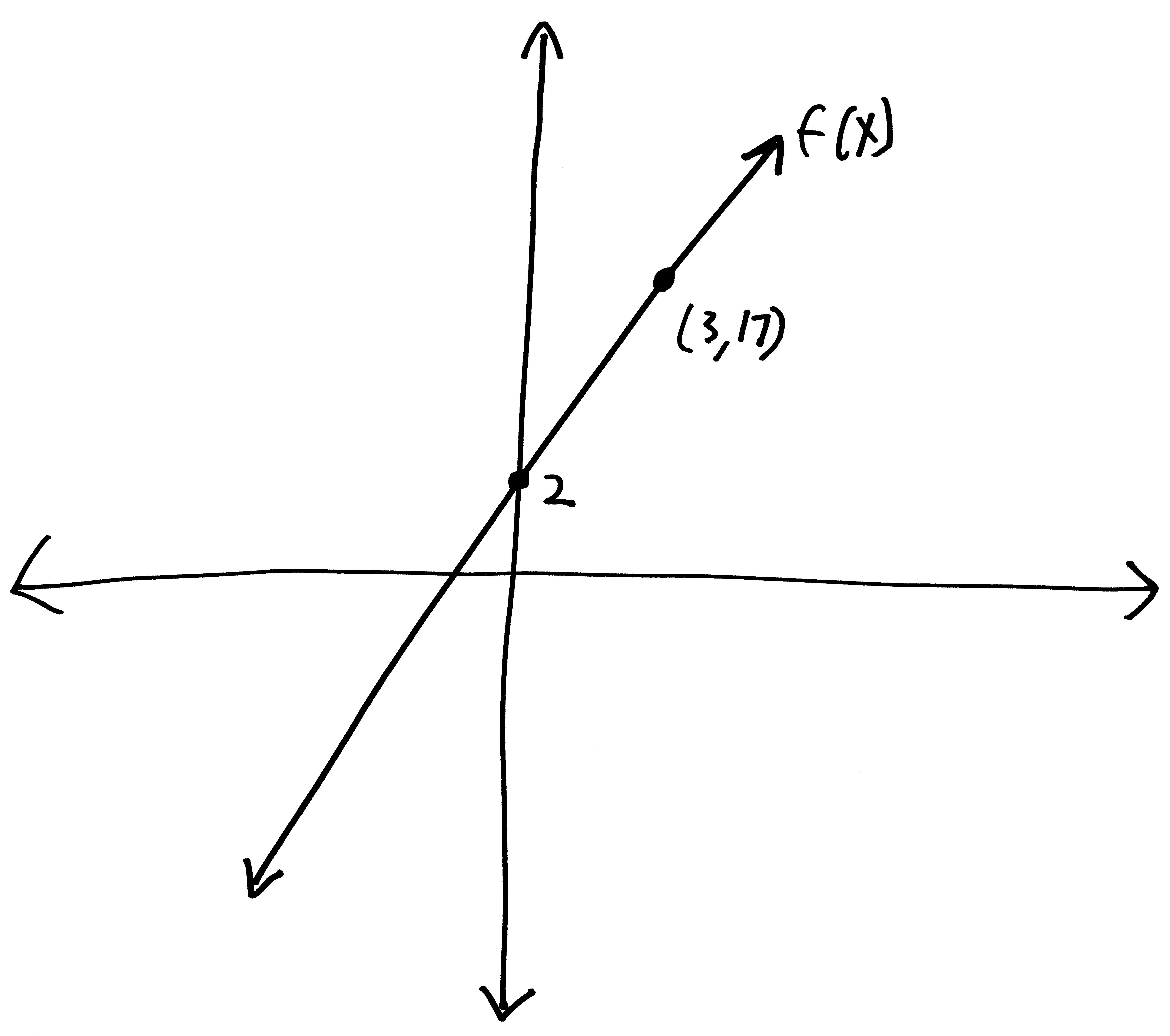
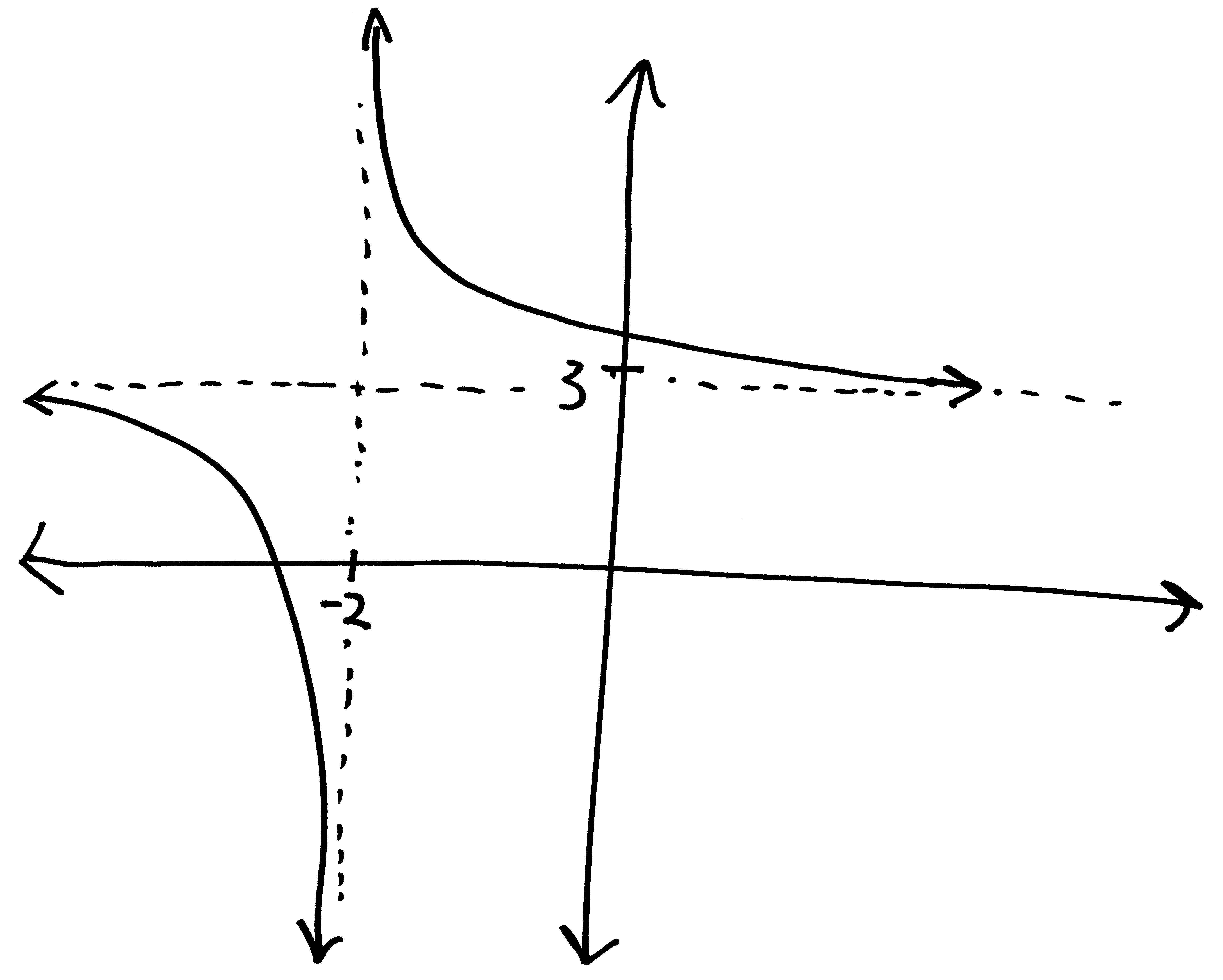
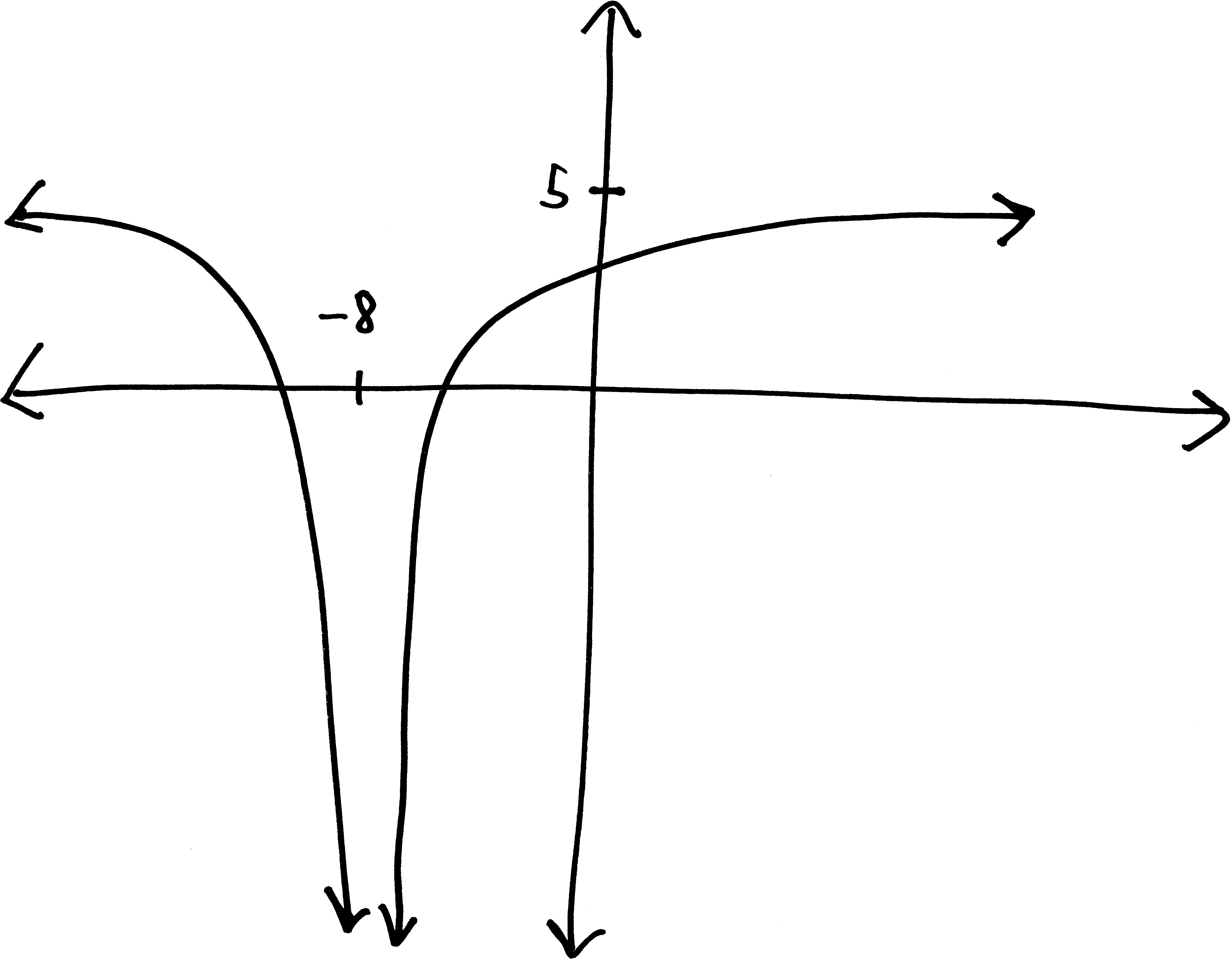
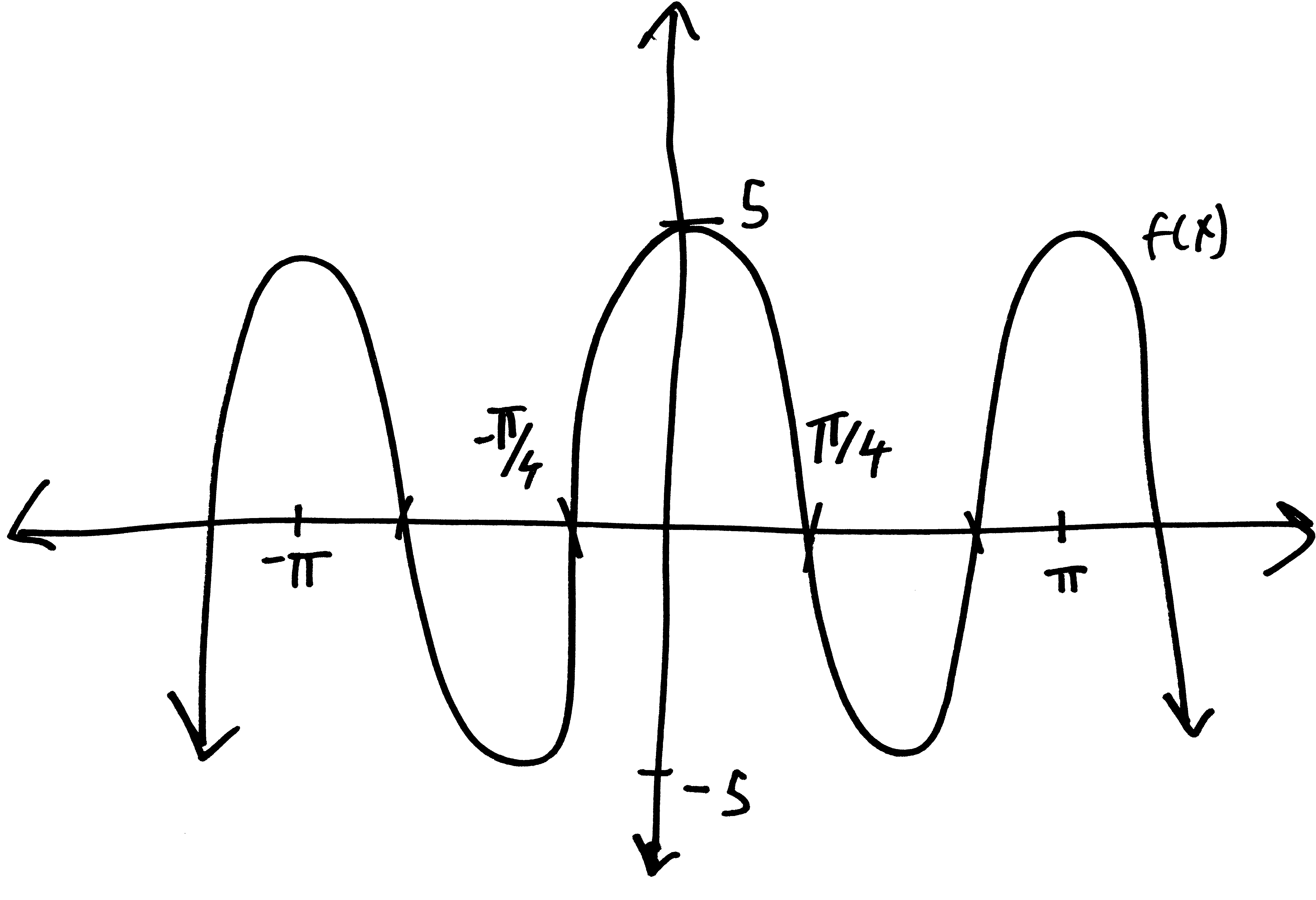
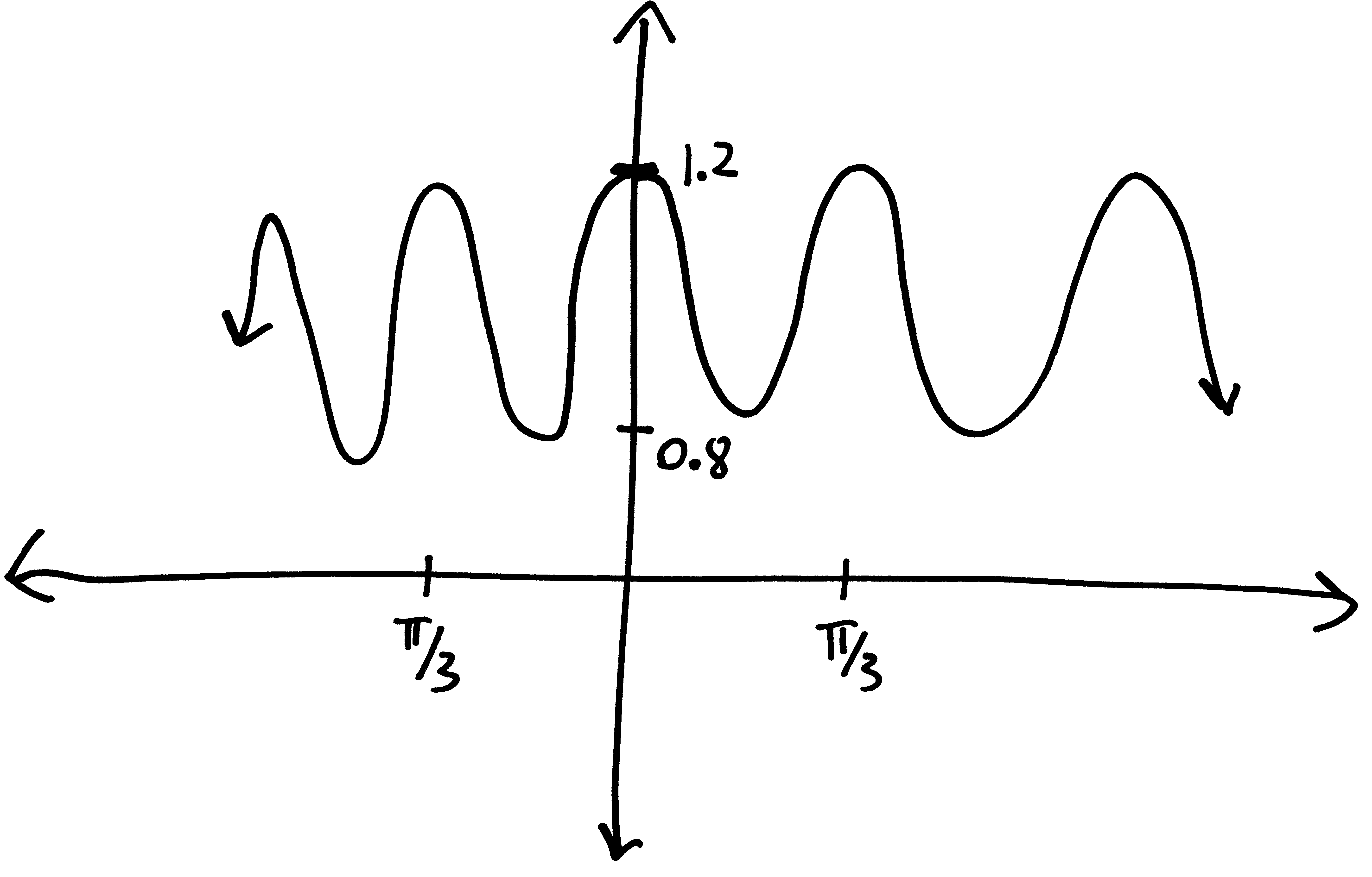
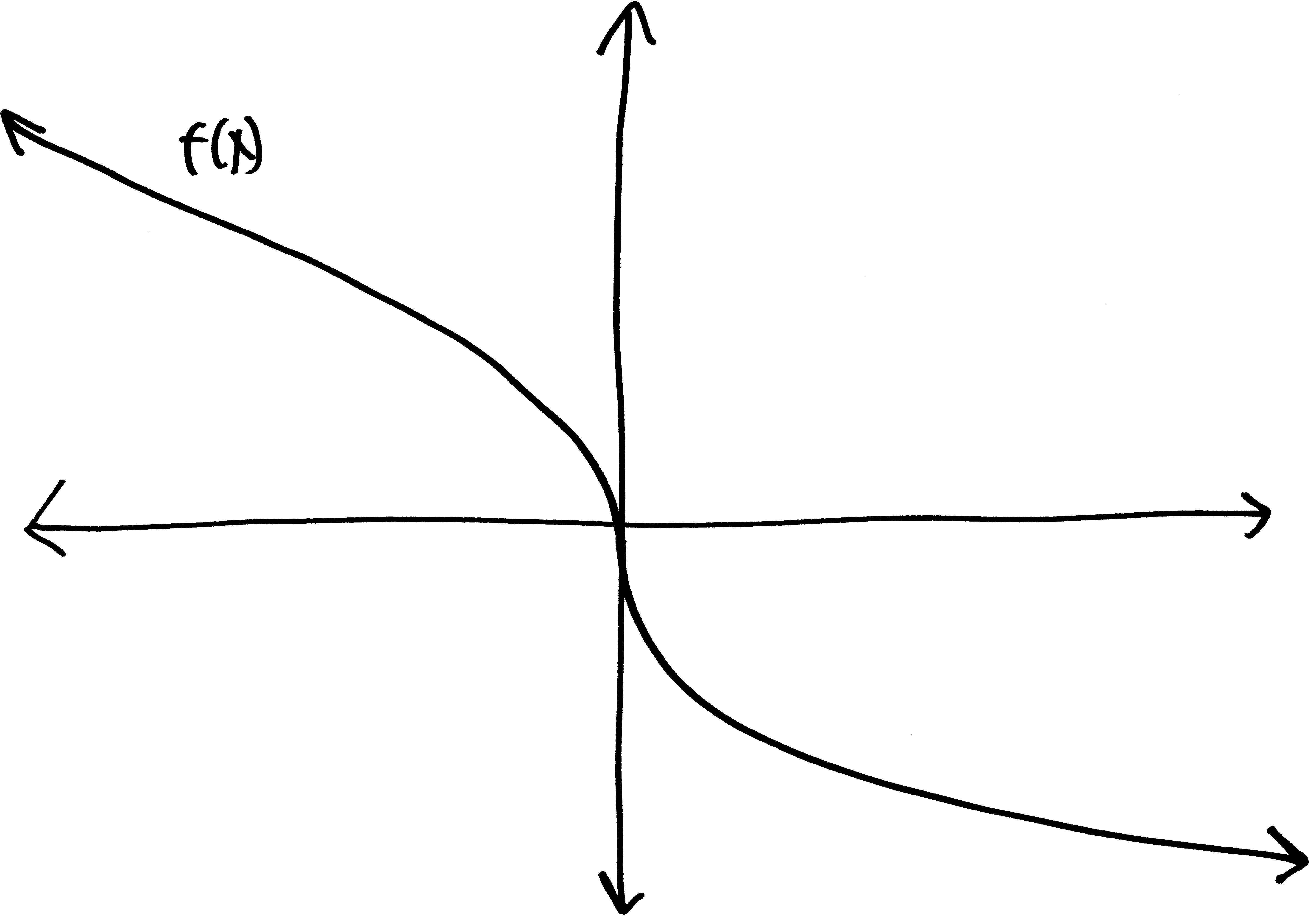
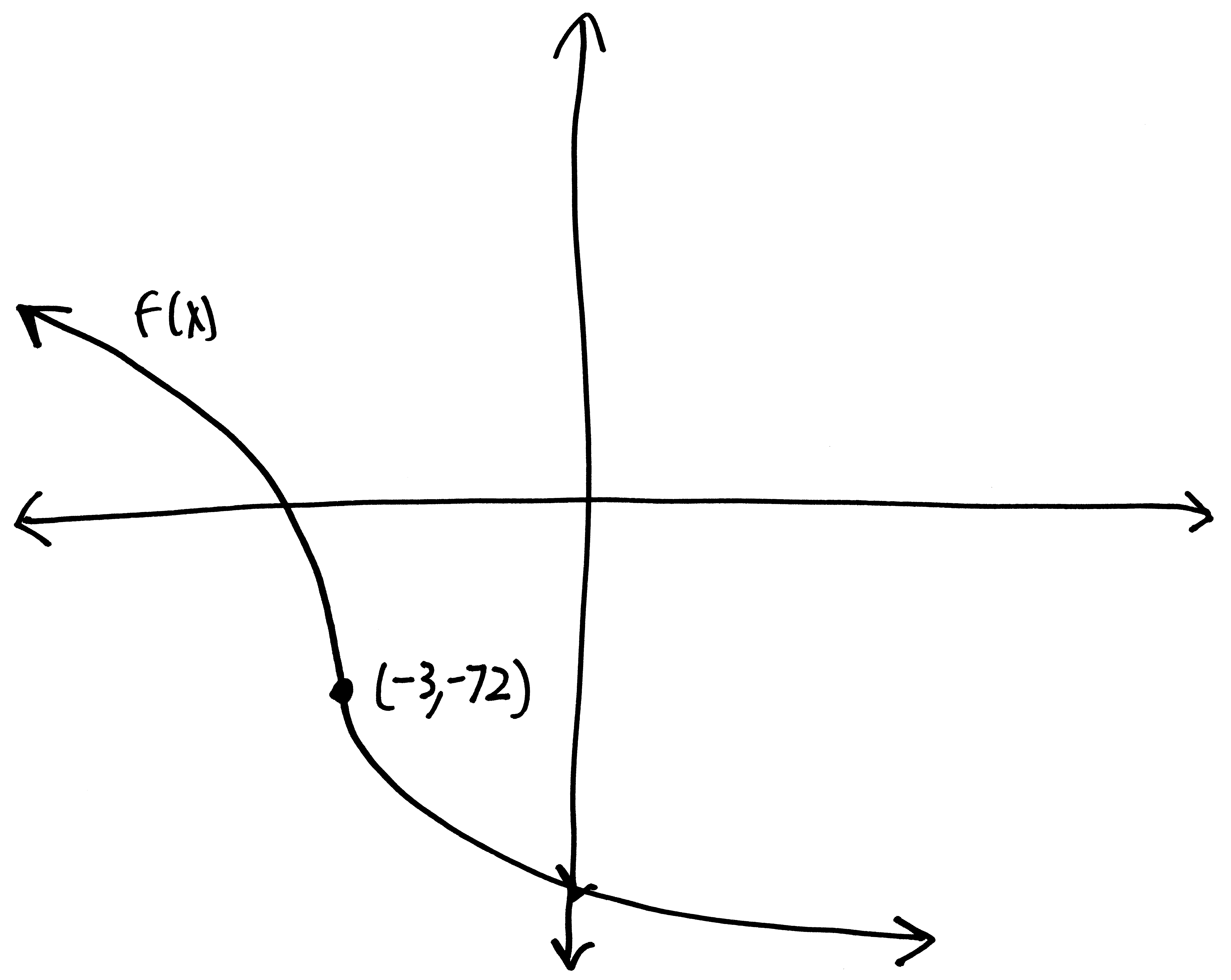
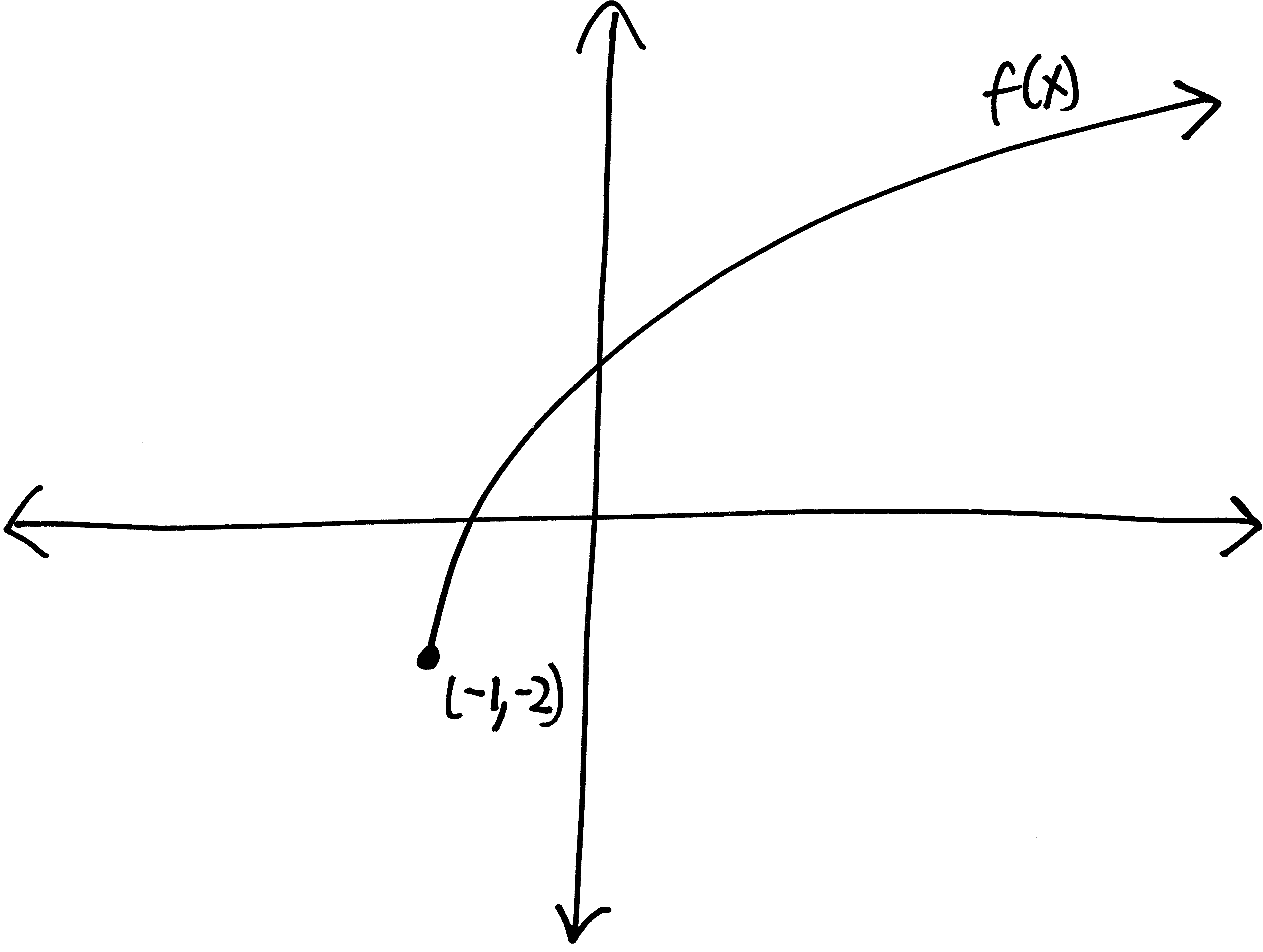
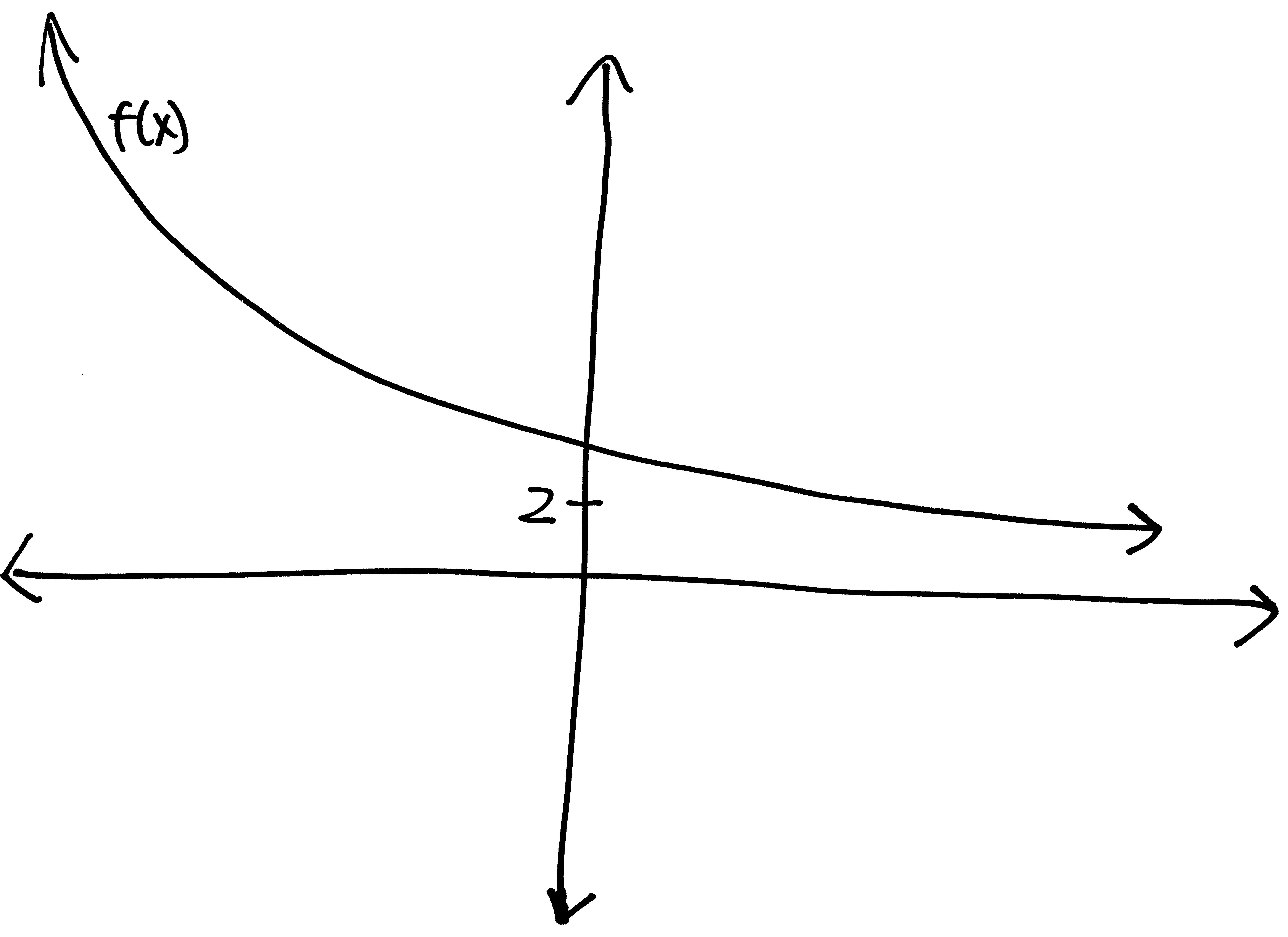
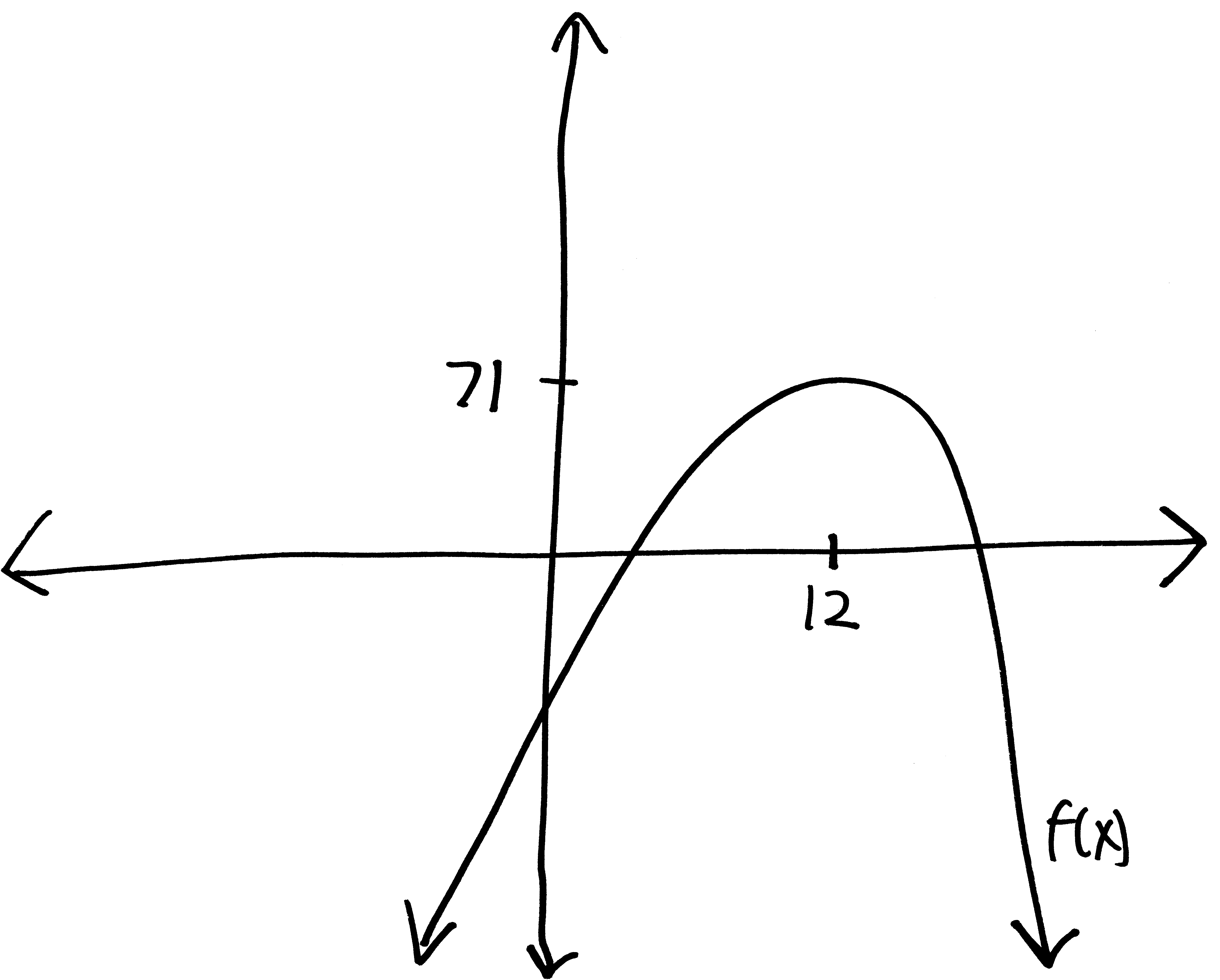
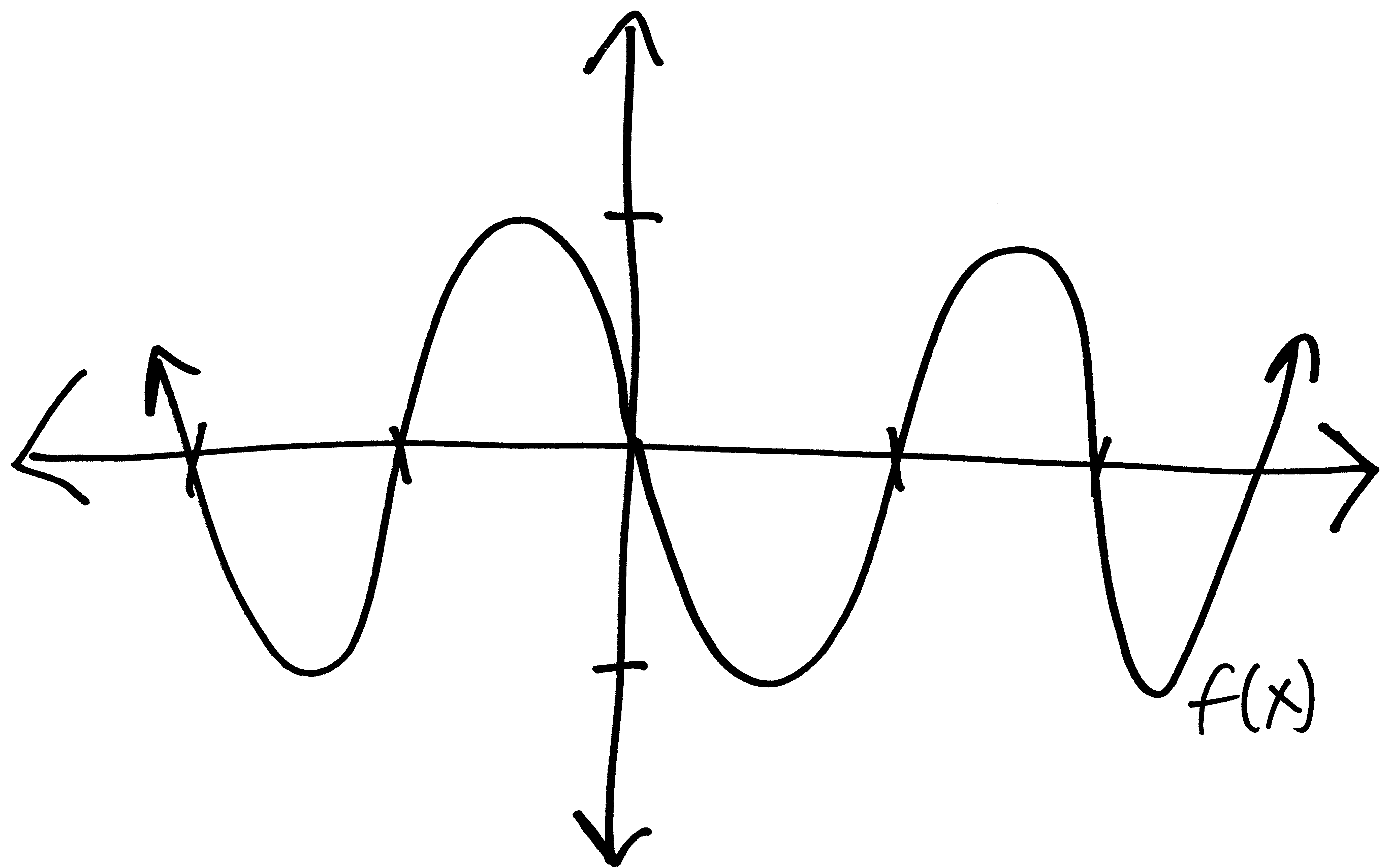
Let’s go from pictures to equations! For each of the following problems:

1. Identify the parent function (or rather, what one of the possible parent functions could be)
2. Describe the transformations that take the parent function to the graph given.
3. List the transformations, in order.
4. Finally (and most importantly), write out a possible equation for this picture. If multiple equations might work, give at least two possibilties.

\end{document}